I wanted to brush up on some algebra I had studied several years back which has by now inadvertently dampened with neglect. I'll start from the basics and build up to the Fundamental Theorem of Finite Abelian Groups. Slow motion, see me let go.

We start with the Isomorphism theorems as generalized by Noether, Artin, et al.
Theorem 1. (First Isomorphism Theorem) Let $\varphi : G \to G'$ be a group homomorphism. Then we have a commutative diagram of groups and group homomorphisms

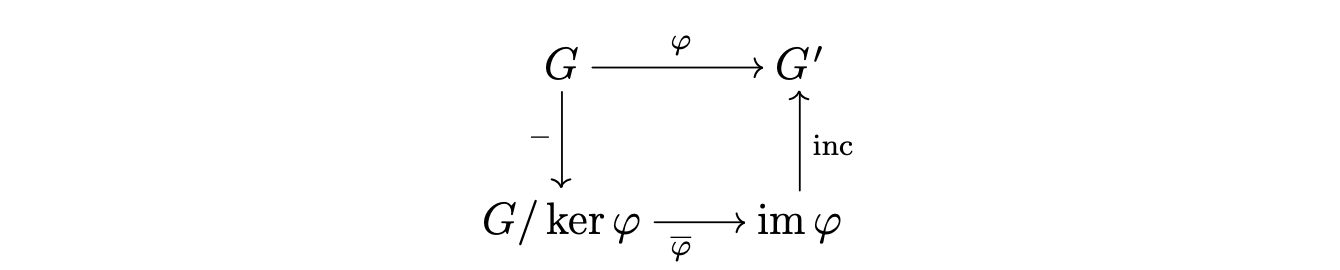
with $\bar{}$ a group epimorphism, $\bar{\varphi}$ a group isomorphism between $G/ \ker \varphi$ and $\text{im} \varphi$ and $\text{inc}$ a group monomorphism.

The proof is trivial since $\ker \varphi \triangleleft G.$

Example. Let $G$ be a group. The map $\theta : G \to \text{Aut}(G)$ given by $x \mapsto (\theta_x : g \mapsto xgx^{-1})$ is a group homomorphism. If $\theta_x = 1_G$, the identity map on $G$, then $xgx^{−1} = g$, i.e., $xg = gx$ for all $g \in G$.
Therefore, $\ker \theta = Z(G)$, the center of $G$. By the First Isomorphism Theorem, $\theta$ induces an isomorphism $\bar{\theta} : G/Z(G) → \text{Inn}(G)$.

The question that arises is regarding the converse, that is, when does the coset $G/H$ have a group structure endowed on it given that the canonical surjection $\bar{} : G \to G/H$ is a group epimorphism? The answer is, of course, when $H = \ker \bar{}$. Let's write it out.

Theorem 2. Let $G$ be a group and $H$ a normal subgroup of $G$. Then $G/H$ is a group under the binary operation $\cdot : G/H \times G/H \to G/H$ given by $(aH, bH) \mapsto abH$. If this is the case then $\bar{} : G → G/H$ is a group epimorphism with kernel $H$.

Proof. We have to check two things: first, that the map $\cdot$ is well defined, and second, that $G/H$ follows the laws of groups.
Suppose that $aH = a'H$ and $bH = b'H$. We have to show that $abH = a'b'H$. Or, equivalently, we must show that if $a'^{−1}a, b'^{−1}b \in H$, then $x = (a'b')^{−1}ab \in H$. But of course $$x = b'^{−1}a'^{-1}ab = b'^{−1}a'^{-1}a (b' b'^{-1})b = (b'^{−1}a'^{-1}a b')(b'^{-1}b)$$ which is in $H$ due to its normality in $G$.
Now, if $a, b, c \in G$, $$aH \cdot (bH \cdot cH) = aH
\cdot bcH = abcH = abH \cdot cH = (aH \cdot bH) \cdot cH,$$ thus showing associativity, the unity is clearly $e_{G/H} = H = e_{G}H$ and $(aH)^{−1} = a^{−1}H$. Thus $G/H$ is a group and we are done. $\square$

We call $G/H$ the quotient or factor group of $G$ by $H$.
We shall now prove some important results.

Theorem 3. (General Cayley Theorem) Let $H$ be an arbitrary subgroup of a group $G$. Let $S = G/H$, the set of left cosets of $H$ in $G$. For each $x \in G$, let $\lambda_x : S \to S$ be defined by $gH \mapsto xgH$. Then $\lambda_x$ is a permutation and the map $\lambda : G \to \Sigma(S)$ given by $x \mapsto \lambda_x$ is a group homomorphism satisfying the following two properties:
(1) $\ker \lambda \subset H$.
(2) $\ker \lambda$ is the unique largest normal subgroup of $G$ contained in $H$, i.e., if $N \triangleleft G$ and $N \subset H$ then $N \subset \ker \lambda$.

Proof. Clearly $\lambda_x$ is a permutation since its inverse is $\lambda_{x^{-1}}$.
Now, for all $x, y \in G$, we have $\lambda_{xy}(gH) = xygH = \lambda_x(ygH) = \lambda_x \lambda_y(gH)$ for all $g \in G$, so $\lambda$ is a group homomorphism and $ker \lambda \triangleleft G$. If $x \in \ker \lambda$, then $xgH = \lambda_x(gH) = gH$ for all $g \in G$. In particular, $xH = H$ so $x \in H$. Finally, suppose that $N \triangleleft G$ with $N \subset H$. To show $N \subset \ker \lambda$, we must show if $x \in N \subset H$, then $\lambda_x$ is $1_S$, the identity map on $S$. So let $x \in N$ and $g \in G$. As $g^{−1}xg \in N$, we have $xg \in gN \subset gH$. Therefore, $xgH = gH$, i.e., $\lambda_x(gH) = gH$ for all $g \in G$. Consequently, $\lambda_x = 1_S$ as required. $\square$

The special case where $H = 1$ gives us:
Corollary 4. (Cayley’s Theorem) Let $G$ be a group, then the map $\lambda : G \to \Sigma(G)$ given by $x \mapsto (\lambda_x : g \mapsto xg)$ is a group monomorphism. In particular, if $G$ is a finite group of order $n$ then there exists a monomorphism $G \to S_n$.

To keep in mind for when studying representation theory of finite groups, the monomorphism $G \to S_n$ is called the (left) regular representation of $G$, and is useful in classification of finite groups. In particular, it shows that every abstract group can be realized by a ‘concrete’ group, for example, a permutation group.

Corollary 5. Let $H$ be a subgroup of a group $G$ with $H < G$. If there exists no normal subgroup $N$ of $G$ satisfying $1 < N \subset H$ then $\lambda : G \to \Sigma(G/H)$ by $x \mapsto (\lambda_x : aH \mapsto xaH)$ is a monomorphism.

Proof. This is immediately obvious since $\ker \lambda$ is the maximal such normal subgroup.

Corollary 6. Let $G$ be a finite group, $H$ a subgroup of $G$ satisfying $|G| \nmid [G : H]!$. Then there exists a normal subgroup $N$ of $G$ satisfying $1 < N \subset H$. In particular, $G$ is not a simple group.

Proof. Let $[G:H] = m$. Then, by Cayley's theorem we have a group homomorphism $\lambda: G \to \Sigma(G/H) \cong S_m$, and $\ker \lambda \triangleleft G$. Also, $\lambda(G)$ is isomorphic to a subgroup of $S_m$, and hence $|\lambda(G)| \mid m!$. Now, if $|G| \nmid m!$, then $|G| > |\lambda(G)|$ which means we $\ker \lambda$ is nontrivial, and hence $G$ is not simple. $\square$

Theorem 7. (First Sylow Theorem) Let $G$ be a finite group, $p$ a prime such that $p^s \mid \mid |G|$ (that is, $p^s \mid |G|$ but $p^{s+1} \nmid |G|$). Then $G$ contains a subgroup of order $p^s$.

I have never attempted or even bothered looking at proofs of Sylow's theorems, and I'm not feeling particularly masochistic, so you and I are both just going to have to take this one as gospel.

Corollary 8. Let $G$ be a finite group. Suppose $p$ is the smallest prime dividing the order of $G$. Suppose also that there exists a subgroup $H$ of $G$ of index $p$. Then $H \triangleleft G$.

Proof. Let $G = m\cdot p^s$ with $p < m$ and $p \nmid m$. We have $[G:H] = p$. Again, consider the homomorphism $\lambda: G \to \Sigma(G/H) \cong S_p$. By Cauchy's theorem, $K = \ker \lambda \triangleleft G$, and by the First Isomorphism Theorem $\lambda(G) \cong G/K$. Let $[H:K] = k$, and then our goal is to show that $k = 1$. We have, $[G:K] = [G:H] \cdot [H:K] = p \cdot k$, which means, $kp \mid \frac{|G|}{|K|}$, that is $kp \mid m \cdot p^s$, or $k \mid m \cdot p^{s - 1}$. But since $m \cdot p^{s - 1}$ has no divisors smaller than $p$, we must have $k = 1$, and we are done. $\square$

Now we move onto some results surrounding the Correspondence Principle, and the other two Isomorphism theorems. I shall begin by stating a couple set theoretic properties of functions which are self-evident and thus don't warrant a proof.

Let $f : A \to B$ be a set map, $C \subset A$, and $D \subset B$ subsets, then:
1. $C \subset f^{−1}(f(C))$, with equality if $f$ is one-to-one.
2. $f(f^{−1}(D)) \subset D$ with equality if $f$ is onto.

Theorem 9. (Correspondence Principle) Let $\varphi : G \to G'$ be a group epimorphism. Then
(1) If $A$ is a subgroup of $G$ (respectively, a normal subgroup), then $\varphi(A)$ is a subgroup of $G'$ (respectively, a normal subgroup). In particular, group epimorphisms preserve normality.
(2) If $A$ is a subgroup of $G$ containing $\ker \varphi$, then $\varphi^{−1}(\varphi(A)) = A$.
(3) If $B$ is a subgroup of $G'$ (respectively, a normal subgroup), then $\varphi^{−1}(B)$ is a subgroup of $G$ (respectively, a normal subgroup) containing $\ker \varphi$ and satisfies $B = \varphi(\varphi^{−1}(B))$.
In particular, if$$\mathcal{G}_{\ker \varphi} := \{A | A \subset G \textit{ a subgroup with } \ker \varphi \}$$$$\mathcal{G}' := \{B | B \subset G' \textit{ a subgroup} \},$$then$$\mathcal{G}_{\ker \varphi} \to \mathcal{G}'$$given by $$A \mapsto \varphi(A)$$
is a bijection of sets preserving inclusions with inverse $B \mapsto \varphi^{−1}(B)$ and restricting to a bijection on normal subgroups.

Proof. These claims are immediately intuitive––we just have to be careful to check such results, since this is the danger of the subject: often what one might expect to be true turns out to be not necessarily true, or in some cases turns out to be completely false. Let $K = \ker \varphi$.
(1). Let $A \subset G$ be a subgroup, then $\varphi|_{A} : A \to G'$ is a group homomorphism, so $\varphi(A) = \text{im} \varphi|_{A} \subset G'$ is a subgroup. Next suppose that $A \triangleleft G$ and $y \in G'$. As $\varphi$ is surjective, $y = \varphi(x)$ for some $x \in G$. Hence $y\varphi(A)y^{−1} = \varphi(x)\varphi(A)\varphi(x)^{−1} = \varphi(xAx^{−1}) = \varphi(A)$. Therefore, $\varphi(A) \triangleleft G'$.
(2). By the first property above, $A \subset \varphi^{−1}(\varphi(A))$, so it suffices to show if $K \subset A$, then $\varphi^{−1}(\varphi(A)) \subset A$. Suppose that $x \in \varphi^{−1}(\varphi(A))$. By definition, $\varphi(x) = \varphi(a)$ for some $a \in A$, hence $e_{G'} = \varphi(a)^{−1}\varphi(x) =
ϕ(a^{−1}x)$. Thus $a^{−1}x \in K$, and so $x \in aK \subset A$.
(3). Let $B$ be a subgroup of $G'$. If $x, y \in \varphi^{−1}(B)$, we have $\varphi(xy^{−1}) = \varphi(x)\varphi(y)^{−1} \in B$, so $\varphi^{−1}(B)$ is a subgroup of $G$. If $k \in K$ then $\varphi(k) = e_{G'} \in B$, so $K \subset \varphi^{−1}(B)$. As $\varphi$ is onto, $B = \varphi(\varphi^{−1}(B))$ by the second property above. Finally, suppose that $B \triangleleft G'$. Let $x \in A$, then $\varphi(x \varphi^{−1}(B)x^{−1}) = \varphi(x)\varphi(\varphi^{−1}(B)) \varphi(x)^{−1} = \varphi(x)B\varphi(x)^{−1} = B$. Hence $x\varphi^{−1}(B)x^{−1} \subset \varphi^{−1}(B)$, so $\varphi^{−1}(B) \triangleleft G$. $\square$

Theorem 10. (Third Isomorphism Theorem) Let $G$ be a group with normal subgroups $K$ and $H$ satisfying $K \subset H$. Then the map $\varphi : G/K \to G/H$ defined by $xK \mapsto xH$ is a group epimorphism with kernel $H/K$ and induces an isomorphism $\bar{\varphi} : (G/K)/(H/K) \to (G/H).$

Proof. Since $K$ and $H$ are normal subgroups of $G$, $G/H$ and $G/K$ are groups. If $xK = yK$ then $y^{−1}x \in K \subset H$, hence $xH = yH$. Therefore, $\varphi$ is well-defined and clearly surjective. As $\varphi(xKyK) = \varphi(xyK) = xyH = xHyH = \varphi(xK)\varphi(yK)$, the map $\varphi$ is a group homomorphism. If $xK \in \ker \varphi$ then $H = e_{G/H} = \varphi(xK) = xH$, so $x \in H$, i.e., $xK \in H/K$. Conversely, if $x \in H$ then $\varphi(xK) =
xH = H = e_{G/H}$, so $xK \in \ker \varphi$. The theorem then completely follows from the First Isomorphism Theorem. $\square$

If $H_1$ and $H_2$ are subgroups of a group $G$, we define $H_1H_2$ as $$H_1H_2 := \{h_1h_2 | h_i ∈ H_i, i = 1, 2\}.$$ Note that this structure is in general not a group. We now give the Second Isomorphism Theorem which helps deal with special cases of this algebraically, though it is undeniably hard to visualize.

Theorem 11. (Second Isomorphism Theorem) Let $G$ be a group and $H$ and $N$ be subgroups with $N$ normal in $G$. Then
(1) $H \cap N \triangleleft H$.
(2) $HN = NH$ is a subgroup of $G$.
(3) $N \triangleleft HN$.
(4) $H/H \cap N \cong HN/N$.
In particular, if $H_1$ and $H_2$ are finite subgroups of $G$, then $|H_1H_2| = |H_1||H_2|/|(H_1 \cap H_2|$.

This means we have

Proof. (1). $H \cap N$ is a subgroup of $H$ and is a normal subgroup in $H$ since $N$ is normal in $G$ and $H$ is normal in $H$.
(2). As $aN = Na$ for all $a \in G$ the sets $HN$ and $NH$ are equal, so we need only show it is a group. Let $h_1, h_2 \in H$ and $n_1, n_2 \in N$. We must show $(h_1n_1)(h_2n_2)^{−1}$ lies in $HN$. But, $$(h_1n_1)(h_2n_2)^{−1} = h_1n_1n_{2}^{−1}h_{2}^{−1} = (h_1n_1n_{2}^{−1}h_{1}^{−1})(h_1h_{2}^{−1})$$ lies in NH = HN.
(3). Clearly. (I don't like the usage of “it's immediately obvious”, “clearly”, etc. in Mathematics, unless it unequivocally requires no additional explanation, and I try to avoid these phrases as much as I can.)
(4). Let $\varphi : H \to HN/N$ by $x \mapsto xN.$ As $\varphi(xy) = xyN = xNyN = \varphi(x)\varphi(y)$ for all $x, y$ in $N$, the map is a homomorphism. We show $\ker \varphi = H \cap N$. If $x \in \ker \varphi \subset H$, then $N = e_{HN/N} = \varphi(x)$ so $x \in N$. Conversely, if $x \in H \cap N$, then $N = xN = \varphi(x)$ and $x \in \ker \varphi$. By definition $HN/N = \{hnN | h \in H, \in N\} = \{hN | h \in H\}$, so $\varphi$ is surjective with kernel $H∩N$. Finally, by the First Isomorphism Theorem, $\varphi$ induces an isomorphism $\bar{\varphi} : H/H \cap N → HN/N$ and we are done. $\square$

We will now discuss some results about finite abelian groups, though, as one might suspect, these are special cases of much more general results.

Lemma 12. Let $G$ be an abelian group and $H_1$, $H_2$ finite subgroups of relatively prime order. Then $H_1H_2 = H_2H_1$ is a group and if further $H_1 \cap H_2 = 1$, then $|H_1H_2| = |H_1||H_2|$. Moreover, if the groups $H_1$ and $H_2$ are both cyclic, then so is $H_1H_2$.

Proof. $G$ is abelian and so both $H_1$ and $H_2$ are normal subgroups. By the Second Isomorphism Theorem, $H_1H_2 = H_2H_1$ is a group. Also, if $H_1 \cap H_2 = 1$, we have $|H_1H_2| = |H_1||H_2|/|H_1 \cap H_2| = |H_1||H_2|$. Finally, if $H_1$ and $H_2$ are both cyclic, we have $H_1 = \langle p \rangle$ and $H_2 = \langle q \rangle$, and then $H_1H_2 = \langle pq \rangle$ is cyclic since order of $pq$ is $|H_1||H_2|$. $\square$

Proposition 13. Let $G$ be a finite abelian group and $p > 0$ a prime dividing the order of G. Then there exists an element of $G$ of order $p$.

Proof. $G$ has no nontrivial subgroups if and only if $G \cong \mathbb{Z}/p\mathbb{Z}$ for some prime $p$, so we assume that $|G|$ is not a prime. In particular, $G$ has a subgroup $1 < H < G$. If $p \mid |H|$, we are done by induction on $|G|$, so we may assume $p \nmid |H$|. Then, there exists a prime $q \neq p$ such that $q \mid |H|$. By induction on $|G|$, there exists an element $y \in H$ of order $q$. As $G$ is abelian, $\bar{G} = G/\langle y \rangle$ is a group. Let $\bar{}: G \to \bar{G}$ be the canonical epimorphism. Since $|\bar{G}| < |G|$ and $p \mid |\bar{G}|$ by Lagrange’s Theorem, or more precisely by the Fundamental Theorem of Cyclic Groups, there exists an element $z$ in $G$ such that $\bar{z}$ has order $p$ in $\bar{G}$. It follows that $z^p$ lies in the kernel of $\bar{}: G \to \bar{G}$, so $z^p = y^i$ for some $i$, hence $z^q$ has order $p$ in $G$. $\square$

What we have just proven is actually Sylow's First Theorem for the case when $G$ is abelian. Cool. Let me also say a word about Sylow's theorems, because they comprise along with Lagrange's result the two most important tools for group theorists, namely, in that, where Lagrange's Theorem gives necessary conditions for subgroups in groups, Sylow's Theorems give sufficient conditions.

Theorem 14. Let $G$ be a finite abelian group and $p > 0$ a prime dividing $|G|$, say $|G| = p^nm$ with $p$ and $m$ relatively prime. Then $$G(p) := \{x \in G \mid x^{p^{r}} = e, r \in \mathbb{Z} \} \triangleleft G$$ and $$|G(p)| = p^n.$$ Moreover, $G(p)$ is the unique subgroup of G of order $p^n$.

Proof. $G(p)$ is a subgroup of $G$ and normal as $G$ is abelian. As every element in $G(p)$ has order a power of $p$, it follows by proposition 13 that $|G(p)| = p^r$ some $r \geq 1$ and by Lagrange’s Theorem that $r \leq n$. In particular, if $x$ lies in $G(p)$, then $x^{p^{n}} = e$. We need to show that $r = n$. Suppose to the contrary that we have $r < n$. Set $\bar{G} = G/G(p)$ and let $\bar{} : G → \bar{G}$ be the canonical epimorphism. By the Correspondence Principle, $p \mid |\bar{G}|$, hence by proposition 13, there exists an element $x \in G \backslash G(p)$ and an integer $m > 0$ such that $$\bar{x}^{p^{m}} = e, \text{ i.e. }, x^{p^{m}} \in G(p).$$ As $x^{p^{n+m}} = (x^{p^{m}})^{p^{n}} = e$, we have $x \in G(p)$, a contradiction. Thus $|G(p)| = p^n$ as desired.
If H is subgroup of $G$ of order $p^n$ , then $HG(p)$ is a subgroup of $G$ of order $|H||G(p)|/|H \cap G(p)| \geq p^n$ by the Second Isomorphism Theorem. It follows that $|H| = |H \cap G(p)| = |G(p)| = p^n$, hence $H = H \cap G(p) = G(p)$. $\square$

Corollary 15. Let $G$ be a finite abelian group of order $n = p_1^{m_1} \cdot \ldots \cdot p_r^{m_r}$ with positive primes $p_1 < \ldots < p_r$ and positive integers $m_1, \ldots , m_r$. Then $G = G(p_1)\ldots G(p_r)$. Moreover, $G \cong G(p_1)\times \ldots \times G(p_r)$.

Proof. As $G(p_1)\ldots G(p_r)$ is a group and we know that $$|G(p_1)\ldots G(p_r)| = |G(p_1)|\cdot \ldots \cdot |G(p_r)|$$ by Lemma 12, the first statement follows by the theorem. The map $$G(p_1)\times \ldots \times G(p_r) \to G$$ given by $$(x_1, \ldots , x_r) \mapsto x_1 \cdot \ldots \cdot x_r$$ is a group homomorphism as $G(p_i)G(p_j) = G(p_j)G(p_i)$ for all $i$ and $j$. Suppose that $x_1 \cdot \ldots \cdot x_r = e$ with $x_i \in G(p_i)$ for $i = 1, \ldots , r$. As $x_j^{n/p_{i}^{m_{i}}} = e$ for all $j \neq i$ and $p$ divides the order of $x_i$, it follows that $x_i = e$ for all $i$. Thus the map is a monomorphism and by counting an isomorphism. $\square$

Notation: It makes sense to write for $H + K$ for additive subgroups in place of $HK$, and moreover $H \oplus K$ for when $H \cap K = \{0\}$. We know that $H + K = H \oplus K$ when $H$ and $K$ are of relatively prime order. Finally, for a prime $p > 1$, a nontrival group of order a power of $p$ is called a p-group.

Lemma 16. Let $G$ be a finite additive $p$-group and suppose that the element $x$ in $G$ has maximal order. Then there exists a subgroup $H$ of $G$ satisfying $G = \langle x \rangle \oplus H$.

Proof. Let $p^n$ be the order of $x$. By the Well-ordering Principle, there exists a maximal subgroup $H$ of $G$ satisfying $H \cap \langle x \rangle = \{0\}$. Therefore, $\langle x \rangle + H = \langle x \rangle \oplus H$, and we are done if $\langle x \rangle + H = G$. So, suppose not. Let $\bar{G} = G/(\langle x \rangle + H)$ and $\bar{} : G \to \bar{G}$ the canonical epimorphism. By Proposition 13, there exists an element $y \in G$ satisfying $y \notin \langle x \rangle + H$ and $\bar{y}$ has order $p$ in $G$. In particular, $py$ lies in $\langle x \rangle + H$. Write $$(*) \hspace5mm py = lx + h \text{ with } l \geq 0 \in \mathbb{Z} \text{ and } h \in H.$$ It follows that $p^ny = p^{n−1}lx + p^{n−1}h$. Since $x$ has maximal order $p^n$ among all elements in $G$, we have $0 = p^ny = p^{n−1}lx+p^{n−1}h$. Therefore, $p^{n−1}lx = −p^{n−1}h$ and it lies in $\langle x \rangle \cap H = \{0\}$. It follows that $p \mid l$, say $l = l'p$. Thus $(*)$ becomes
$$(\triangle) \hspace5mm py = l'px + h \text{ or } p(y − l'x) = h \in H.$$ As $y \notin \langle x \rangle + H$, we must have $y − l'x \notin \langle x \rangle + H$. The maximality of $H$ now yields $$\langle y − l'x, H \rangle ∩ \langle x \rangle \neq \{0\}.$$ Therefore, there exist integers $r$, $s$ with $r \neq 0$ satisfying $$0 \neq rx = s(y − l'x) + h' \text{ for some } h' \in H.$$ Hence $sy = rx + sl'x − h'$ lies in $\langle x \rangle + H$. We look at the integer $s$. If $p \mid s$, then by $(\triangle)$, we have $s(y − l'x)$ lies in $H$. This implies that $rx$ lies in $\langle x \rangle \cap H = \{0\}$, a contradiction.
If $p \nmid s$, then $p$ and $s$ are relatively prime, so there exists an equation $1 = pa + sb$ for some integers $a$ and $b$. Since both $py$ and $sy$ lie in $\langle x \rangle + H$, we have $y = apy + bsy$ lies in $\langle x \rangle + H$, which is a contradiction. The lemma then follows. $\square$

Corollary 17. Let $G$ be a finite $p$-group. Then $G$ is a product of cyclic $p$-groups.

Proof. Assume that $G$ is additive but not cyclic. In particular $|G| > p$. By lemma 16, $G = \langle x \rangle \oplus H$ for some $x \in G$ and subgroup $H$ of $G$. Since $G$ is not cyclic, $H \neq G$, and the result follows by induction on $|G|$. $\square$

Proposition 18. Every finite abelian group is a product of cyclic groups.

Proof. By Corollary 15 every finite abelian group is a product of finite abelian $p$-groups. By Corollary 17, every finite abelian $p$-group is a product of cyclic $p$-groups. $\square$

Theorem 19. (Fundamental Theorem of Finite Abelian Groups) Let $G$ be a finite additive group and for each prime $p > 0$ dividing $G$, let $G(p)$ be the unique $p$-subgroup of $G$ of maximal order. Then
$$G = \bigoplus_{p \mid |G|}G(p).$$ Moreover, if $p \mid |G|$, then $$G(p) \cong \times_{i = 1}^r \mathbb{Z}/p^{n_i}\mathbb{Z}$$ with $r$ unique and $1 \leq n_1 \leq \cdots \leq n_r$ also unique relative to this ordering. In particular, any finite abelian group is a product of cyclic $p$-groups for various primes $p$.

Proof. Let $p \mid |G|$. By Corollary 15 and Proposition 18, it suffices to show $G(p) \cong \times_{i=1}^r \mathbb{Z}/p^{n_i}\mathbb{Z}$ and uniquely up to isomorphism.
As every abelian $p$-group is isomorphic to a product of cyclic $p$-groups by Corollary 17 and every cyclic $p$-group must be isomorphic to $\mathbb{Z}/p^a\mathbb{Z}$ for some integer a, to finish, it suffices to show that if $$(*) \hspace5mm \times_{i=1}^r \mathbb{Z}/p^{n_i}\mathbb{Z} \cong \times_{j=1}^s \mathbb{Z}/p^{m_j}\mathbb{Z}$$ with $n_1 \geq \dots \geq n_r$ and $m_1 \geq \dots \geq m_s$, then $r = s$ and $n_i = m_i$ for all $i$. We may assume that the number $N$ of the $n_i$ that are equal to $1$ is less than the number $M$ of the $m_j$ that equal $1$. In particular, $p^N \leq p^M$. Multiplying $(*)$ by $p$, we see that$$\times_{i=N+1}^r \mathbb{Z}/p^{n_i−1}\mathbb{Z} \cong \times^s_
{j=M+1}\mathbb{Z}/p^{m_j−1}\mathbb{Z}$$as $p(\mathbb{Z}/p^k\mathbb{Z}) \cong \mathbb{Z}/p^{k−1}\mathbb{Z}$ for all $k$. By induction, $n_i − 1 = m_i − 1$ for all $i > N$. As $|G(p)| = \prod^r_{i=1} p^{n_i} = \prod^s_{i=1} p^{m_j}$, we conclude that $r = s$ and $n_i = m_i$ for all $i$ and we are done. $\square$

What was it all for? Well, remember, groups are merely abstract objects. You can write their elements as $\{ a, b, c\}$ or $\{1, 2, 3\}$, it does not matter. The rules of the group are what in fact determine the group, not its particular representation. The map is not the territory, this is not a pipe. What this entire formalization aims to arrive at is to determine all finite abelian groups up to isomorphism, and in doing so, to reduce it to the study of groups of order a power of a prime. Why primes? I suspect because just as how primes build up larger numbers, we sought a similar expression of duality in the construction of larger groups using basic building blocks arising out of primes.

Next, I'm thinking I'll do one post on Hilbert's basis theorem and Nullstellensatz, then one more post summarizing the main result of Galois theory, and then, once my cleavers will have been sharpened again, move onto what I anticipate to be an extremely protracted series on the Weil conjectures. Zealous goals seem to sprout up each time I get any free time on my hands, but admittedly I have a poor history of coming through. We shall see how this goes.